Suma de fracciones con el mismo denominador
Para sumar fracciones con el mismo denominador se tienen que sumar los numeradores dejando el mismo denominador.
Como las 2 fracciones tienen el mismo denominador, lo que tenemos que hacer es dejar el mismo denominador, que es 4, y sumar los numeradores:
3 + 2 = 5
Y el resultado de la suma de fracciones es:
Suma de fracciones con distinto denominador
Para hacer suma de fracciones con distinto denominador, lo primero que hay que hacer es poner un denominador común: esto es el mínimo común múltiplo entre los denominadores que haya. Después multiplicamos cada numerador por el número que hayamos multiplicado al denominador. Por último, sumamos los numeradores que hayamos obtenido y dejamos el mismo denominador.
Lo primero es haya un denominador común entre el 3 y el 5. Para eso, hallamos el mínimo común múltiplo entre ambos.
m.c.m. (3,5) = 15
Por lo tanto 15 es el denominador común de las dos fracciones.
Ahora tenemos que multiplicar cada numerador por el número que hayamos multiplicado el denominador. Para ello, dividimos el m.c.m entre el denominador inicial y el resultado lo multiplicamos por el numerador de esa fracción:
Para la primera fracción:
15 : 3 = 5
5 x 2 = 10
Por lo tanto, 10 es el numerador de la primera fracción.
Para la segunda fracción:
15 : 5 = 3
3 x 4 =12
Por lo tanto, 12 es el numerador de la segunda fracción.
Ahora ya solo nos queda sumar los numeradores:
10 + 12 = 22
Y el resultado de la suma de fracciones es:
RESTA
para ello, primero tienes que saber qué es el denominador y el numerador de una fracción:
El numerador es el número que se escribe en la parte superior de la fracción y el denominador es el número que se escribe en la parte inferior de la fracción.

Ahora ya sólo te queda saber que para hacer una resta de fracciones es necesario que las fracciones tengan el mismo denominador. Una vez que las fracciones tengan el mismo denominador tan solo tenemos que restar los numeradores.
¿Qué hacemos si las fracciones tienen distinto denominador? En este caso, tenemos que poner el mismo denominador haciendo el mínimo común múltiplo (m.c.m.) entre ellos.
Vamos a verlo con un ejemplo:
Como los denominadores son distintos, 4 y 6, tenemos que hallar el mínimo común múltiplo entre ellos.
Las dos nuevas fracciones tendrán como denominador 12.
Para hallar el numerador de cada nueva fracción se divide el nuevo denominador (el m.c.m. que habíamos hallado) entre el antiguo denominador y el resultado se multiplica por el antiguo numerador.
La primera fracción:
La segunda fracción:
La resta de fracciones queda ahora:
Como las dos fracciones tienen el mismo denominador, podemos hacer la resta: restamos los numeradores y dejamos el mismo denominador:
Y el resultado de la resta de fracciones es un doceavo.
MULTIPLICACIÓN
Para ello, tan solo tenemos que seguir los siguientes pasos:
- Simplificar fracciones: Cualquier numerador se puede simplificar con cualquier denominador.
- Multiplicar en línea: Se multiplican los denominadores para obtener el denominador final y se multiplican los numeradores para obtener el numerador final.
Por ejemplo,
Primero debemos simplificar las fracciones para que resulte más fácil multiplicar después. Por lo tanto, para simplificar lo que haremos será descomponer cada número en factores primos.
4 = 2 x 2
8 = 2 x 2 x 2
15 = 3 x 5
9 = 3 x 3
8 = 2 x 2 x 2
15 = 3 x 5
9 = 3 x 3
Y sustituimos cada número de las fracciones por sus factores primos.
Ahora simplificamos, tachando los numeradores y denominadores que sean iguales. Y nos queda que el resultado de la multiplicación es 5/6.
Cómo se hace una multiplicación de fracciones con un número entero:
Cuando queremos multiplicar una fracción por un número entero es muy sencillo, simplemente el número entero lo pasamos a fracción poniendo como denominador un 1.
La fracción 3/6 se puede simplificar como hemos visto en el ejemplo anterior descomponiendo en factores primos y nos queda 1/2.
El número entero 7 lo pasamos a fracción poniendo un 1 como denominador: 7/1.
Ahora multiplicamos en línea: multiplicamos denominadores: 2 x 1 = 2.
Multiplicamos numeradores: 1 x 7 = 7
De esta manera, nos queda la fracción: 7 / 2
DIVISIÓN
Ya sabes que la expresión es otra forma de representar la operación Por lo tanto, cuando te enfrentes a una división del tipo puedes interpretarla así:
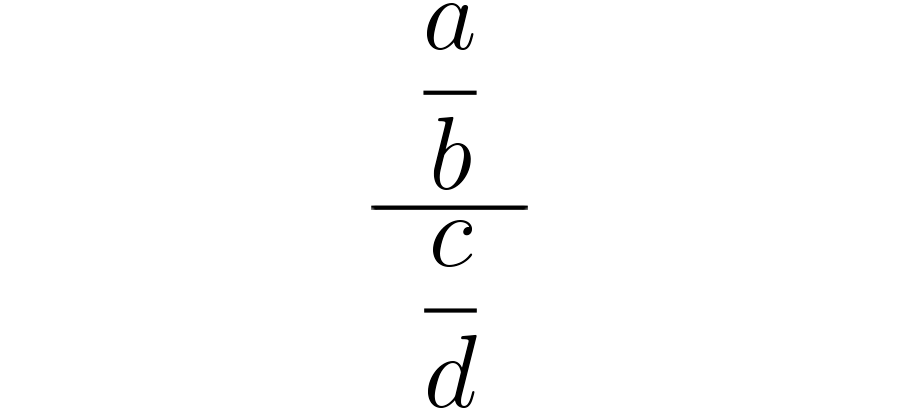
En muchos países se enseña a realizar y recordar cómo hacer esta operación por medio de un procedimiento que se denomina “ley de la oreja” o “ley de extremos y medios”.
Este procedimiento indica que se multiplican los extremos superior e inferior para obtener el numerador, y los números del medio para obtener el denominador.
En la siguiente imagen puedes ver como se hace:
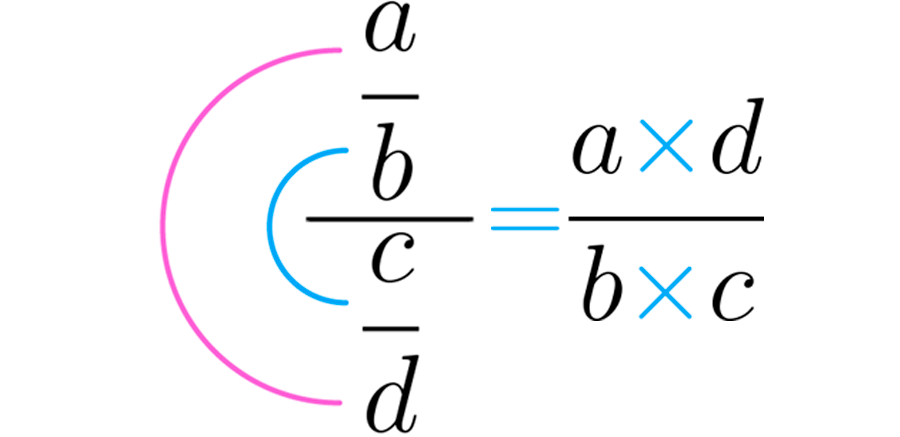
Ahora usemos este método para realizar la división
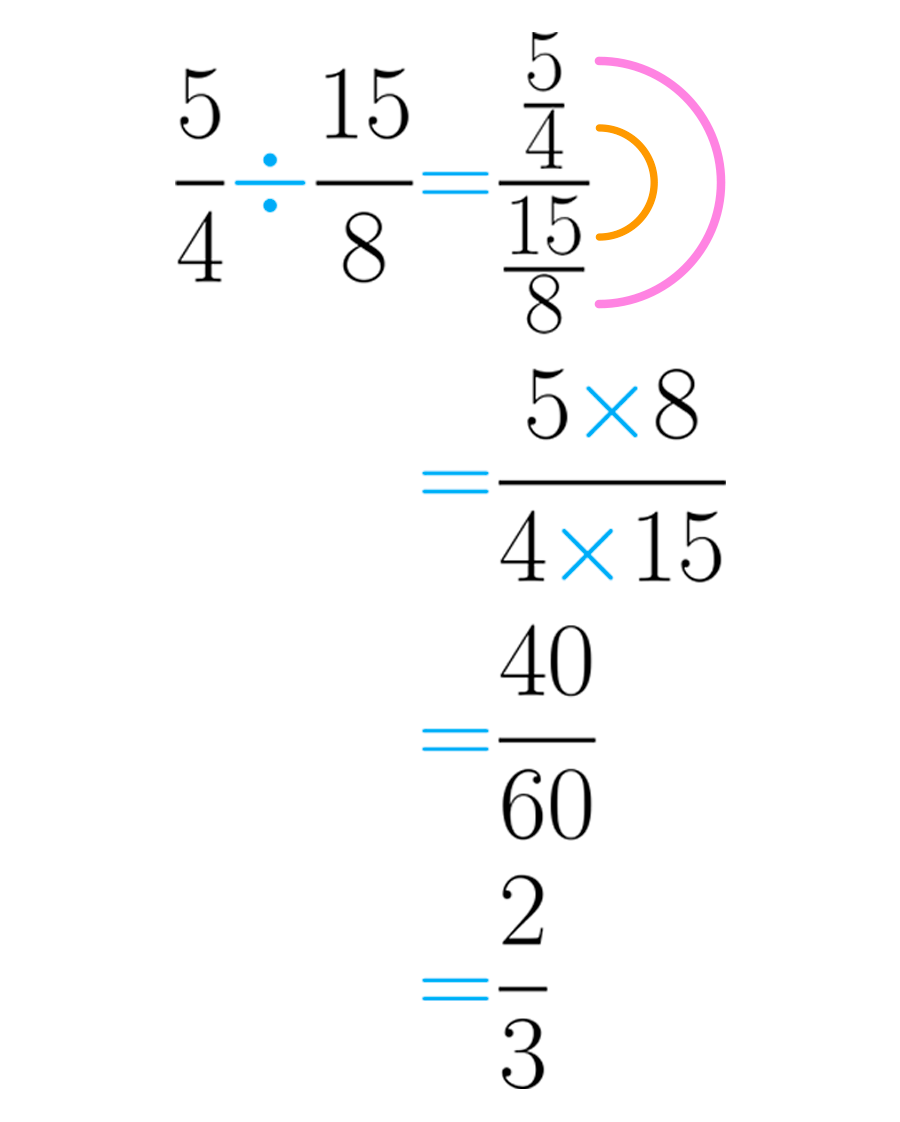
Puedes ver porque se le llama “oreja”, pues recuerda precisamente esta parte de nuestro cuerpo.
El resultado de la división es sin embargo, después de simplificar esta expresión, se obtiene la fracción que es irreducible.
Existe otra forma de realizar la división de fracciones: los “productos cruzados”. Con este método no es necesario poner las fracciones una sobre la otra, simplemente se multiplica numerador por denominador y denominador por numerador. Observa un ejemplo:
Realicemos la operación
Primero multiplica el numerador del dividendo por el denominador del divisor. Este será el numerador de la respuesta. Después multiplica el denominador del dividendo por el numerador del divisor. Este resultado será el denominador del cociente:
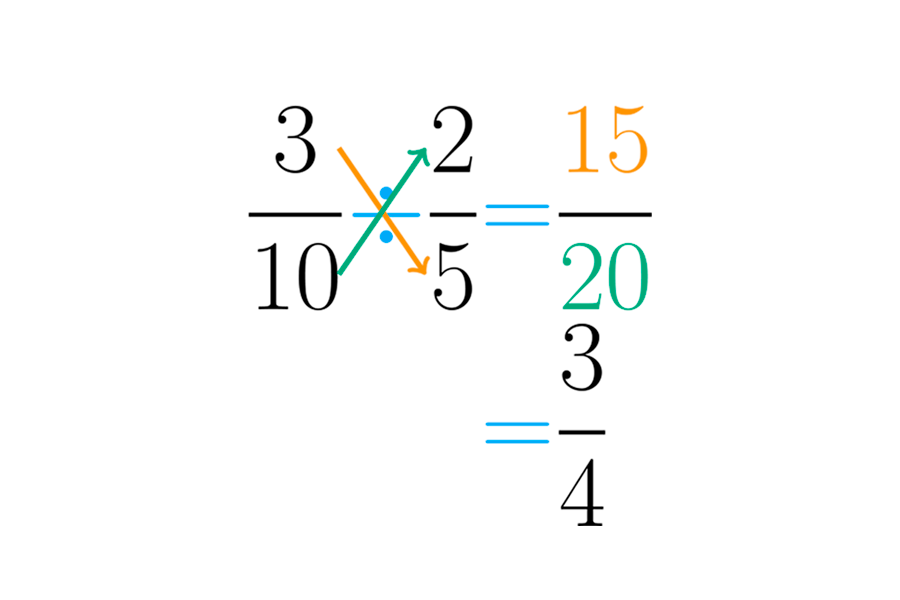
Por supuesto los resultados de obtenidos por la “ley de la oreja” y por los “productos cruzados” son siempre iguales.









Me parece que lo que se muestra aquí se entiende muy bien
ResponderEliminar